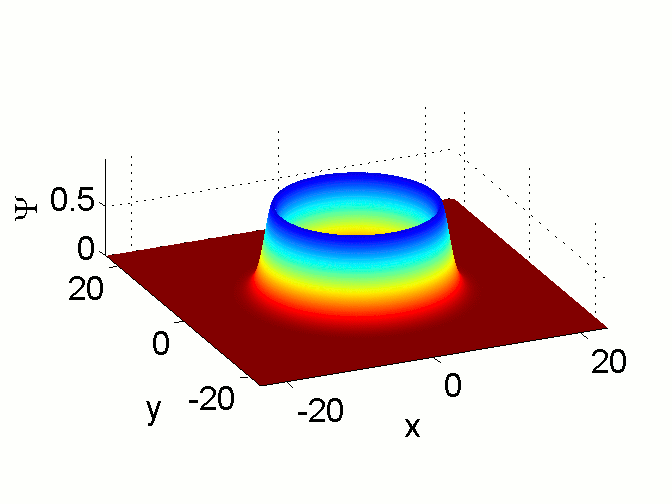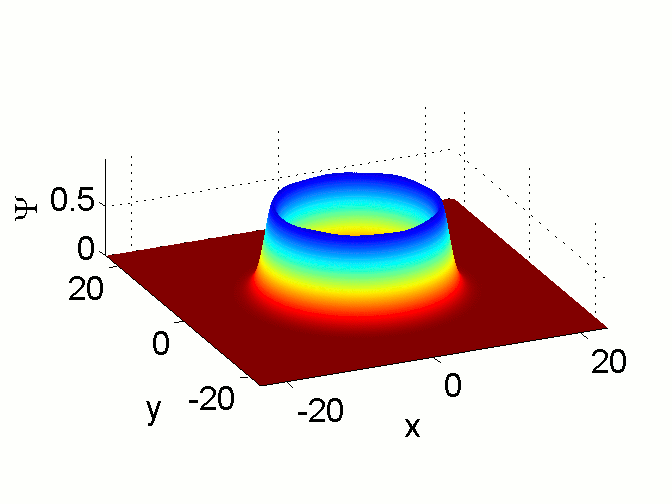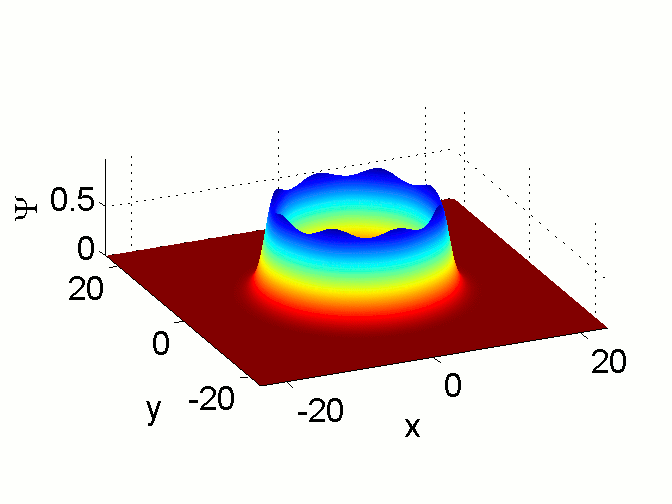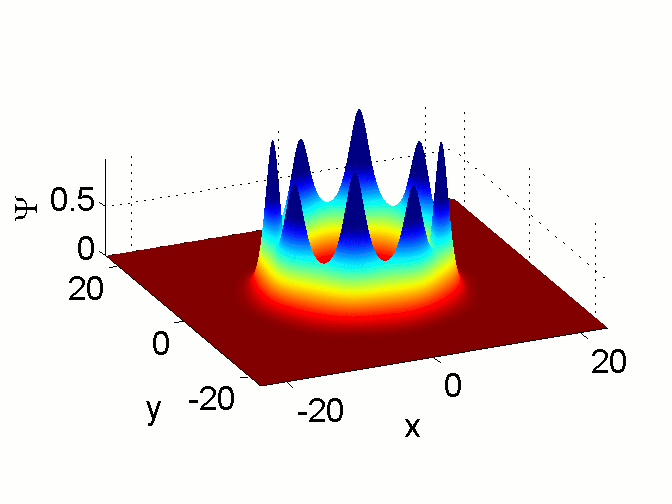SCIENCE SUB-PAGES
Select the sub-page you would like to go to below:
PUBLICATIONS
2026
Advancing Heliophysics and Space Weather Modeling through Open Science
C. Corti, M. M. Kuznetsova, M. Reiss, J. Yue, J. T. Karpen, ..., R. M. Caplan, et. al.
Submitted to Space Weather. (2026). PDF Coming Soon.
2025
Energetic Particles from Quasi-Separatrix Layers and Current Sheets at the Sun
N. A. Schwadron, R. M. Caplan, J. A. Linker, E. Palmerio, and M. A. Young
The Astrophysical Journal. 996,1 (2025). PDF.A Near-real-time Data-assimilative Model of the Solar Corona
C. Downs, J. A. Linker, R. M. Caplan, E. I. Mason, P. Riley, R. Davidson, A. Reyes, E. Palmerio,
R. Lionello, J. Turtle, M. Ben-Nun, M. M. Stulajter, V. S. Titov, T. Torok, L. Upton,
R. Attie, B. K. Jha, C. N. Arge, C. J. Henney, G. Valori, H. Strecker, D. Calchetti, D. Germerott,
J. Hirzberger, D. O. Suarez, J. B. Rodriguez, S. K. Solanki, X. Cheng, and S. Wu
Science. Vol. 388, Issue 6753, pg. 1306-1310 (2025). PDF (Paper). PDF (Materials and Methods). ZIP (Movies).Quantifying Uncertainties in Solar Wind Forecasting Due to
Incomplete Solar Magnetic Field Information
S. G. Heinemann, J. Pomoell, R. M. Caplan, M. J. Owens, S. Jones, L. Upton,
B. K. Jha, and C. N. Arge
The Astrophysical Journal. 986,2 (2025). PDF.Open-source Flux Transport (OFT). I. HipFT - High-performance Flux Transport
R. M. Caplan, M. M. Stulajter, J. A. Linker, C. Downs, L. A. Upton,
B. K. Jha, R. Attie, C.N. Arge, and C. J. Henney
The Astrophysical Journal Supplement Series. 278,24 (2025). PDF.
2024
Portability of Fortran's `do concurrent' on GPUs
R. M. Caplan, M. M. Stulajter, J. A. Linker, J. Larkin, H. A. Gabb, S. Su,
I. Rodriguez, Z. Tschirhart, and N. Malaya
SC24-W: Workshops of the Int. Conf. for High Perf. Comp., Net., Stor., and Anal.,
Atlanta, GA, USA, 2024 WACCPD, pp. 1904-1913 (2024) PDF (arxiv).Coronal Models and Detection of Open Magnetic Field
E. Asvestari, M. Temmer, R. M. Caplan, J. A. Linker, S. G. Heinemann, R. F. Pinto,
C. J. Henney, C. N. Arge, M. J. Owens, M. S. Madjarska, J. Pomoell, S. J. Hofmeister,
C. Scolini, and E. Samara
The Astrophysical Journal. 971,45 (2024) PDF.Quantitative comparisons between WSA implementations
S. I. Jones, R. M. Caplan, C. N. Arge, J. A. Linker, C. J. Henney, R. Attie, C. Downs,
B. K. Jha, J. Turtle, and L. Upton
The Astrophysical Journal. 970,35 (2024) PDF.Heliophysics and Space Weather Information Architecture and Innovative Solutions:
Current Status and Ways Forward
A. Massona, S. F. Fungb, E. Camporealec, M. M. Kuznetsovab, S. Poedtse, J. Barnum,
R. Ringuette, D. D. Zeeuwi, S. Polson, V. M. Sadykov, V. Navarro, B. Thomas,
R. M. Caplan, J. Linker, L. Rastaetter, C. Wiegand, R. M. McGranaghan, M. Petrenko,
C. Didigu, J. Reerink, J. Ireland, and B. Ceccon
Advances in Space Research. In Press, (2024) PDF.Space Weather with Quantified Uncertainties: Improving Space Weather Predictions
with Data-Driven Models of the Solar Atmosphere and Inner Heliosphere
N. V. Pogorelov, C. N. Arge, R. M. Caplan, P. Colella, J. A. Linker, T. Singh, B. V. Straalen,
L. Upton, C. Downs, C. Gebhart
Journal of Physics: Conference Series. ASTRONUM 2023. 2742 (2024) 012013 PDF.Advancing parabolic operators in thermodynamic MHD models II:
Evaluating a Practical Time Step Limit for Unconditionally Stable Methods
R. M. Caplan, C. D. Johnston, L. K. S. Daldoff, and J. A. Linker
Journal of Physics: Conference Series. ASTRONUM 2023. 2742 (2024) 012020 PDF.CORHEL-CME: An Interactive Tool For Modeling Solar Eruptions
J. A. Linker, T. Torok, C. Downs, R. M. Caplan, V. Titov, A. Reyes, R. Lionello, and P. Riley
Journal of Physics: Conference Series. ASTRONUM 2023. 2742 (2024) 012012 PDF.On the Origin of the Sudden Heliospheric Open Magnetic Flux
Enhancement During the 2014 Pole Reversal
S. G. Heinemann, M. J. Owens, M. Temmer, J. A. Turtle, C. N. Arge, C. J. Henney,
J. Pomoell, E. Asvestari, J. A. Linker, C. Downs, R. M. Caplan, S. J. Hofmeister,
C. Scolini, R. F. Pinto, and M. S. Madjarska
The Astrophysical Journal. 965,151 (2024). PDF.Improved modelling of SEP event onset within the WSA–Enlil–SEPMOD framework
E. Palmerio, J.G. Luhmann, L. M. Mays, R. M. Caplan, D. Lario, I.G. Richardson, K. Whitman,
C.O. Lee, B. Sánchez-Cano, N. Wijsen, Y. Li, C. Cardoso, M. Pinto, D. Heyner, D. Schmid,
H. Auster, and D. Fischer
Journal of Space Weather and Space Climate. 14,3 (2024). PDF.SuNeRF: 3D Reconstruction of the Solar EUV Corona Using Neural Radiance Fields
R. Jarolim, B. Tremblay, A. Munoz-Jaramillo, K.-M. Bintsi, A. Jungbluth, M. Santos,
A. Vourlidas, J. P. Mason, S. Sundaresan, C. Downs, and R. M. Caplan
The Astrophysical Journal Letter. 961,L31 (2024) PDF.
2023
Global MHD Simulations of the Time-dependent Corona
R. Lionello, C. Downs, E. I. Mason, J. A. Linker, R. M. Caplan, V. S. Titov, and M. L. DeRosa
The Astrophysical Journal. 959,77 (2023). PDF.Time-dependent Dynamics of the Corona
E. I. Mason, R. Lionello, C. Downs, J. A. Linker, R. M. Caplan, and M. L. DeRosa
Astrophysical Journal Letters. 959,L4 (2023). PDF.Deflection of Coronal Mass Ejections in Unipolar Ambient Magnetic Fields
M. Ben-Nun, T. Torok, E. Palmerio, C. Downs, V. S. Titov, M. G. Linton, R. M. Caplan, and R. Lionello
The Astrophysical Journal. 957,74 (2023). PDF.Improving Coronal Hole Detections and Open Flux Estimates
R. M. Caplan, E. I. Mason, C. Downs, and J. A. Linker
The Astrophysical Journal. 958,43 (2023). PDF.Acceleration of a production Solar MHD code with Fortran standard parallelism:
From OpenACC to `do concurrent'
R. M. Caplan, M. M. Stulajter, and J. A. Linker
13th AsHES Workshop. 2023 IEEE IPDPSW Proceedings., (2023) 582-590. PDF (ArXiv).Review of Solar Energetic Particle Prediction Models
K. Whitman, ..., R. M. Caplan, et. al.
Advances in Space Research. 72 (2023) 5161-5242. PDF.
2022
Can Fortran's `do concurrent' Replace Directives for Accelerated Computing?
M. M. Stulajter, R. M. Caplan, and J. A. Linker
Accelerator Programming Using Directives. WACCPD 2021.
Lecture Notes in Computer Science, 13194, 3-21 (2022). Springer, Cham. PDF.Comparing and Contrasting the Properties of the Inner Heliosphere
for the Three Most Recent Solar Minima
P. Riley, R. M. Caplan, C. Downs, J. A. Linker, and R. Lionello.
JGR: Space Physics. 127,8 (2022) e2022JA030261. PDF.
2021
Coronal Hole Detection and Open Magnetic Flux
J. A. Linker, S. G. Heinemann, M. Temmer, M. J. Owens, R. M. Caplan, C. N. Arge,
E. Asvestari, V. Delouille, C. Downs, and S. J. Hofmeister.
The Astrophysical Journal. 918,1 (2021) 21. PDF.Variations in Finite Difference Potential Fields
R. M. Caplan, C. Downs, J. A. Linker, and Z. Mikic.
The Astrophysical Journal. 915,1 (2021) 44. PDF.Using Parker Solar Probe observations during the first four perihelia to
constrain global magnetohydrodynamic models
P. Riley, R. Lionello, R. M. Caplan, C. Downs, J. A. Linker, S. Badman, and M. L. Stevens
Astronomy & Astrophysics. 650 (2021) A19. PDF.Energetic Proton Propagation and Acceleration Simulated for the
Bastille Day Event of July 14, 2000
M. A. Young, N. A. Schwadron, M. Gorby, J. Linker, R. M. Caplan, C. Downs,
T. Török, P. Riley, R. Lionello, V. Titov, R. A. Mewaldt, C. M. S. Cohen
The Astrophysical Journal. 909,2 (2021) 160. PDF.
2020
Early Results from the Solar-minimum 2019 Total Solar Eclipse.
J. M. Pasachoff, C. A. Lockwood, J. L. Inoue, E. N. Meadors, A. Voulgaris, D. Sliski, A. Sliski, K. P. Reardon,
D. B. Seaton, R. M. Caplan, C. Downs, J. A. Linker, G. Schneider, P. Rojo, and A. C. Sterling.
Proceedings of the International Astronomical Union. s354,15 (2020) 3-14 PDF.
2019
Can an Unobserved Concentration of Magnetic Flux Above the Poles of the Sun
Resolve the Open Flux Problem?
P. Riley, J. A. Linker, Z. Mikic, R. M. Caplan, C. Downs and J. Thumm.
The Astrophysical Journal. 884,1 (2019) 18. PDF.Predicting the Structure of the Solar Corona and Inner Heliosphere
during Parker Solar Probe's First Perihelion Pass.
P. Riley, C. Downs, J. A. Linker, Z. Mikic, R. Lionello, and R. M. Caplan.
The Astrophysical Journal. 874,2 (2019) L15. PDF.GPU Acceleration of an Established Solar MHD Code using OpenACC.
R. M. Caplan, J. A. Linker, Z. Mikic, C. Downs, T. Torok, and V. S. Titov.
Journal of Physics: Conference Series. ASTRONUM 2018. 1225,1 (2019) 012012 PDF.Coupled MHD-Focused Transport Simulations for Modeling Solar Particle Events.
J. A. Linker, R. M. Caplan, N. Schwadron, M. Gorby, C. Downs, T. Torok, R. Lionello, and J. Wijaya
Journal of Physics: Conference Series. ASTRONUM 2018. 1225,1 (2019) 012007 PDF.
2018
Predicting the Corona for the 21 August 2017 Total Solar Eclipse.
Z. Mikic, C. Downs, J. A. Linker, R. M. Caplan, D. H. Mackay, L. A. Upton, P. Riley, R. Lionello,
T. Torok, V. S. Titov, J. Wijaya, M. Druckmuller, J. M. Pasachoff, and W. Carlos.
Nature Astronomy. 2 (2018) 913-921. ePDF.Sun-to-Earth MHD Simulation of the 14 July 2000 “Bastille Day” Eruption.
T. Torok, C. Downs, J. A. Linker, R. Lionello, V. S. Titov,
Z. Mikic, P. Riley, R. M. Caplan, and J. Wijaya
The Astrophysical Journal. 858,1 (2018) 75. PDF.Regularized Biot-Savart Laws for Modeling Magnetic Flux Ropes.
V. S. Titov, C. Downs, Z. Mikic, T. Torok, J. A. Linker, and R. M. Caplan
The Astrophysical Journal Letters. 852,2 (2018) L21. PDF.
2017
The Open Flux Problem.
J.A. Linker, R.M. Caplan, C. Downs, P. Riley, Z. Mikic, R. Lionello,
C. J. Henney, C. N. Arge, Y. Liu, M. L. Derosa, A. Yeates, and M. J. Owens.
The Astrophysical Journal. 848,1 (2017) 70. PDF.
2016
Advancing parabolic operators in thermodynamic MHD models:
Explicit super time-stepping versus implicit schemes with Krylov solvers.
R. M. Caplan, Z. Mikic, J. A. Linker, and R. Lionello.
Journal of Physics: Conference Series. ASTRONUM 2016. 837,1 (2017) 012016 PDF.Synchronic coronal hole mapping using multi-instrument EUV images:
Data preparation and detection method.
R.M. Caplan, C. Downs, and J.A. Linker.
The Astrophysical Journal. 823,1 (2016) 53. PDF.Properties of the Fast Forward Shock Driven by the July 23 2012 Extreme Coronal Mass Ejection.
P. Riley, R.M. Caplan, J. Giacalone, D. Lario, and Y. Liu.
The Astrophysical Journal. 819,1 (2016) 57. PDF.MHD Simulation of the Bastille Day Event.
J.A. Linker, T. Torok, C. Downs, R. Lionello, V. Titov, R.M. Caplan, Z. Mikic, and P. Riley.
AIP Conference Proceedings, Solar Wind 14. 1720, (2016) 020002. PDF.An Empirically Driven Time-Dependent Model of the Solar Wind.
J. A. Linker, R.M. Caplan, C. Downs, R. Lionello, P. Riley, Z. Mikic, C.J. Henney, C.N. Arge, T. Kim, and N. Pogorelov.
Journal of Physics: Conference Series. ASTRONUM 2015. 719,1 (2016) 012012 PDF.
2014
Scattering and Leapfrogging of Vortex Rings in a Superfluid.
R.M. Caplan, J. D. Talley, R. Carretero-González, and P.G. Kevrekidis.
Physics of Fluids. 26 (2014) 097101. PDF.A Modulus-Squared Dirichlet Boundary Condition for Time-Dependent
Complex Partial Differential Equations and its Application to the Nonlinear Schrödinger Equation.
R.M. Caplan and R. Carretero-González.
SIAM Journal on Scientific Computing. 36,1 (2014) A1-A19 PDF.
2013
NLSEmagic: Nonlinear Schrödinger Equation Multidimensional Matlab-based
GPU-accelerated Integrators using Compact High-order Schemes.
R.M. Caplan.
Computer Physics Communications. 184,4 (2013) 1250-1271. PDF.A Two-Step High-Order Compact Scheme for the Laplacian Operator and its
Implementation in an Explicit Method for Integrating the Nonlinear Schrödinger Equation.
R.M. Caplan and R. Carretero-González.
Journal of Computational and Applied Mathematics. 251 (2013) 33-46. PDF.Numerical Stability of Explicit Runge-Kutta Finite-Difference Schemes
for the Nonlinear Schrödinger Equation.
R.M. Caplan and R. Carretero-González.
Applied Numerical Mathematics. 71 (2013) 24-40. PDF.
Awarded the 6th most successful IMACS paper published in 2013 in Applied Numerical Mathematics.
2012
Existence, Stability, and Scattering of Bright Vortices in the
Cubic-Quintic Nonlinear Schrödinger Equation.
R.M. Caplan, R. Carretero-González, P.G. Kevrekidis, and B.A. Malomed.
Mathematics and Computers in Simulation. 82,7 (2012) 1150-1171. PDF.
2010
Simulating the Nonlinear Schrödinger Equation using the Computational Capability of NVIDIA Graphics Cards
R.M. Caplan and R. Carretero-González.
ACSESS Proceedings. ACSESS 2010, (2010) AP10-04. PDF.
2009
Azimuthal Modulational Instability of Vortices in the
Nonlinear Schrödinger Equation.
R.M. Caplan, Q.E. Hoq, R. Carretero-González, and P.G. Kevrekidis.
Optics Communications. 282,7 (2009) 1399-1405. PDF.Existence of Steady State Bright Vortex Solutions to the Cubic- Quintic Nonlinear Schrödinger Equation
R.M. Caplan and R. Carretero-González.
ACSESS Proceedings. ACSESS 2009, (2009) AP0903. PDF.
Other Works
The Open Flux Problem: The Need for High Latitude Observations.
J.A. Linker, P. Riley, C. Downs, R.M. Caplan, C. DeForest, S.E. Gibson, D.M. Hassler,
J.T. Hoeksema, W.D. Pesnell, X. Sun, and N.M. Viall.
Heliophysics 2024 Decadal Whitepapers. Bulletin of the AAS 55(3) (2023). PDF.From MPI to MPI+OpenACC: Conversion of a legacy FORTRAN
PCG solver for the spherical Laplace equation.
R. M. Caplan, Z. Mikic, and J. A. Linker.
Presented at the 2017 NVIDIA GPU Technology Conference. arXiv:1709.01126 (2017) PDF.
Ph.D. Dissertation
Study of Vortex Ring Dynamics in the Nonlinear Schrödinger Equation utilizingGPU-Accelerated High-Order Compact Numerical Integrators
Ph.D. Dissertation in Computational Science (2012).
Joint program with Claremont Graduate University and San Diego State University.
Committee Chair: Professor Ricardo Carretero.
Abstract▼. DOI: 10.5642/cguetd/52.
Masters Thesis
Azimuthal Modulational Instability of Vortex Solutions to theTwo Dimensional Nonlinear Schrödinger Equation
Masters Thesis in Computational Science (2008).
San Diego State University.
Thesis chair: Professor Ricardo Carretero.
Abstract▼ PDF.